Du tænker måske over, hvem der bruger afstandsbestemmelse/udregning til noget, bortset fra astronomer og matematikere. Det er der mange der gør. Fx tømrere, snedkere, arkitekter osv – hvis man skal designe noget lige fra en specialbygget motorcykel til en bryllupskage kan formlen bruges.

Introduktion

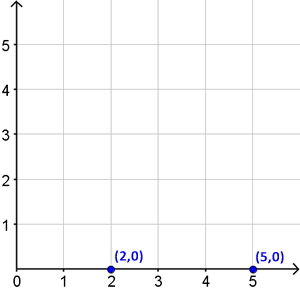
Vi bruger det vi kalder afstandsformlen til at få afstanden mellem to hvilke som helst punkter overhovedet. Lad os sige du har brug for at bestemme afstanden mellem punkterne (2.0) og (5.0).
Sådan her ser de ud i et koordinatsystem:

Bare ved at skæve til koordinatsystemet, kan du se at der er 3 felter imellem. Begge punkter ligger på x-aksen, så det er bare et mål på en lige linje. Faktisk er det ikke engang sikkert, du behøver et koordinatsystem for at regne den ud. Mén, hvordan kan man bestemme afstanden mellem to tilfældige punkter i et koordinatsystem? Det kan man ved hjælp af afstandsformlen.

Et skridt ad gangen

Ved første øjekast ligner formlen et værre rod. Men prøv at tænke på x2-x1 og y2-y1 komponenterne son længden i hver sin retning. Ved at bruge de to værdier, konstruerer vi matematisk en imaginær trekant med to ben, hvis længder vi kan bestemme.

Her kan du se:

Man måler længden langs hver akse, og bruger så Pythagoras læresætning (a i anden plus b i anden = c i anden) til at udregne længden af hypotenusen, som er den imaginære linje direkte mellem vores to punkter. Det spiller ingen rolle hvilket punkt der er hvilket. Selve kernen i dette er, at det eneste der er vigtigt er ændringen i x og y. Man bruger hvert mål som en side i trekanten, hvor hypotenusen er afstanden mellem de to punkter.

Man kunne udtrykke afstanden ved hjælp af en formel sådan her:

Eksempel

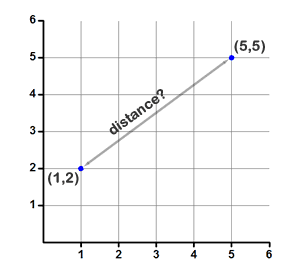
Find afstanden mellem de to punkter (5,5) og (1,2) ved at bruge afstandsformlen.

Løsning:
I stedet for bare blindt at smide tal ind i en formel, så sæt dem ind i et koordinatsystem  så du ved hvad der foregår.

Det her er dine to punkter. Husk at det vigtige er ændringerne i x og y. Her er ændringen i x 4 felter og ændringen i y er 3 felter.  Man kan endda tælle på koordinatsystemet for at være sikker.

Når man kender punkterne, er det bare at sætte dem ind I formlen. Du kan udregne en hvilken som helst linje på denne måde. Husk bare på at hvis du vil udregne hvor langt der er fra København til Odense så bliver det i fugleflugt.

Eksempel uden graf

Find afstanden mellem de to punkter (8,-2) og (3, 9).
Nu hvor du forstår hvordan formlen virker, kan du plotte tallene direkte ind:

Afstandsformlen er ikke kompliceret, du skal bare øve dig med et koordinatsystem, så du kan se hvad der sker. Du laver simpelthen bare en trekant og finder længden på hypotenusen. Det er bare Pytagoras læresætning.